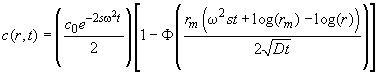
Faxén solutions of the Lamm equation

The simplest approximation of the Lamm equation solution is that by Faxén (1929), which can be written as

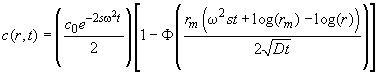
with the meniscus position r_m, the boundary position of a non-diffusing species r*(t)=r_mexp(w²st) and the error function F.  It has a first term describing radial dilution, a second term (1-F) for the diffusional spreading, and the movement of r*(t) describes the boundary movement.  This solution describes qualitatively many features of Lamm equation solutions, in particular curves of the type in example (a).  However, it is quantitatively not very precise, and it does not describe many features of the Lamm equation, such as the accumulation of material at the bottom of the cell, or the interdependence of the effects of diffusional spreading, radial dilution and the radial-dependence of the force. 

Faxén solutions according to can be calculated with the calculator function of Sedfit.

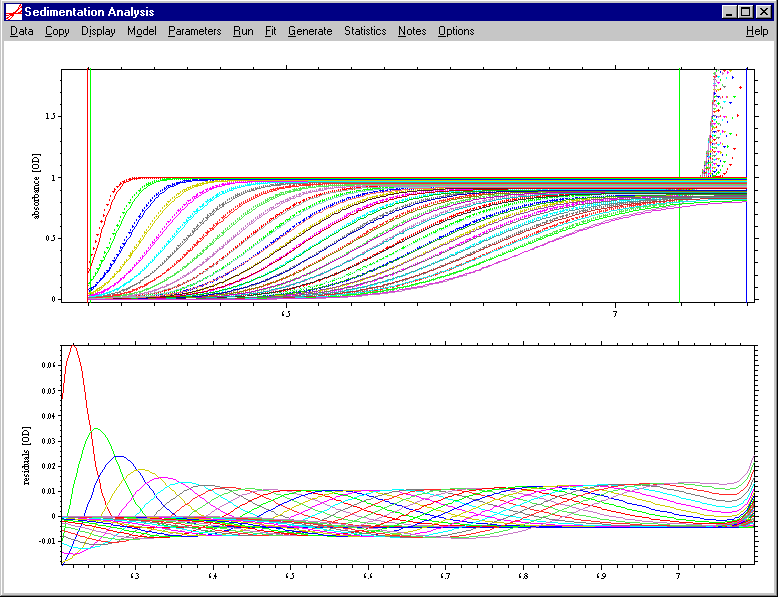
The following is sedimentation profiles simulated with finite element methods (dots), compared with the Faxén solutions (lines) in the top graph, and the residuals in the lower graph. 

This is for a species with 100kDa, 7S, at 30,000 rpm:

this the same at 50,000 rpm:

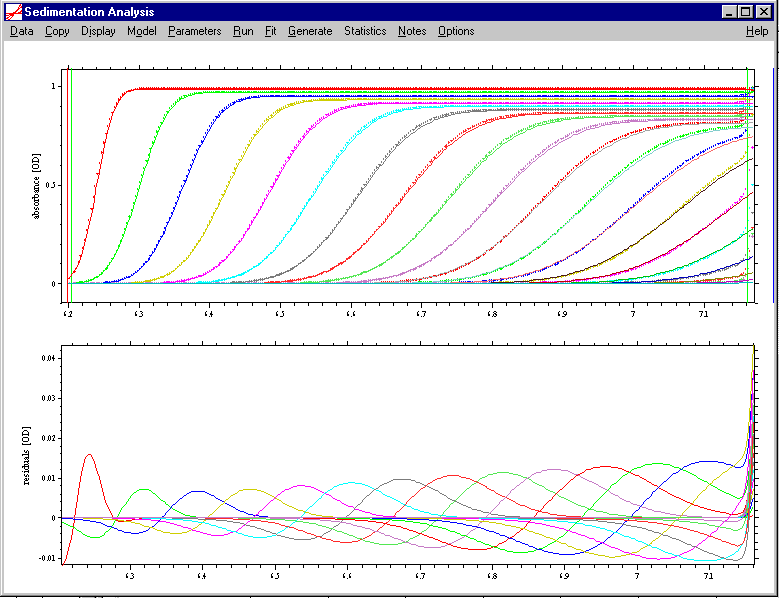
this is for 800kDa, 20S, 50,000 rpm

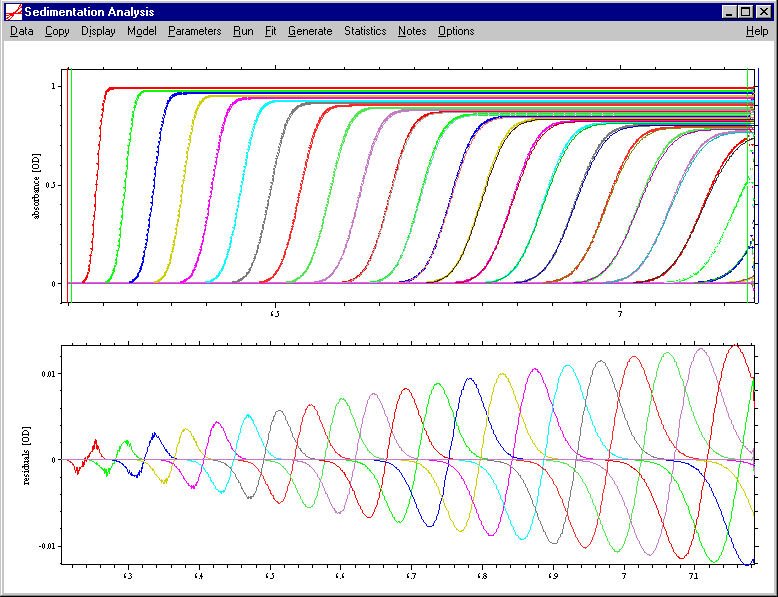
Clearly, the precision of the Faxén solution is not sufficient for the analysis of experimental data.

A different way of using the Faxén approximation is to extract the displacement and the central slope of the sedimentation boundaries from the equation above, and to fit it to a central percentile of the sedimentation boundaries (e.g., fitting only the boundary from 10% - 90% of the plateau value).  This is implemented in SEDPHAT, in the Linear Fractional Boundary model.