Three ternary association models are available:
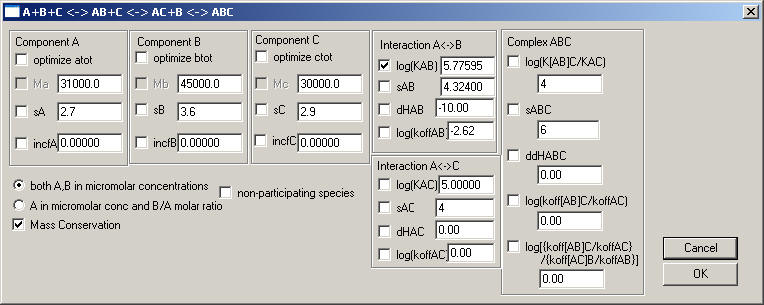
A+B+C <--> AB + C <--> AC + B <--> ABC
A+B+B+C <--> AB +B+C <--> BAB + C <--> AC + B+B <--> ABC + B <--> BABC
A+B+B+C+C <--> A + BC + BC <--> AB +B+C+C <--> BAB + C +C <--> BABC +C <--> CBABC
A+B+C <--> AB + C <--> AC + B <--> ABC
The model implemented is that of a molecule A with two binding sites, one for B and one for C. It can also be used for A with only a single site for which both B and C compete (in this case you need to specify that there's very large negative cooperativity).
There is the possibility of cooperativity, which is expressed quantitatively as the difference in the binding constant of C binding to A, as compared to C binding to AB (with pre-bound B). The number controlling this interaction is the base-10 log of K[AB-C]/K[A-C]. If this cooperativity is regarded as a change of free energy of binding of C to A or AB, there may be an enthalpic component to this cooperativity, which is expressed here as ddHABC, meaning delta-delta H[ABC] = delta H[ABC] - (delta H[AB]+delta H[AC]). Finally, there can be differences in the binding kinetics, expressed here in the form of a coupling constant describing the ratio of rate constants of C dissociating like ABC -> AB + C versus the binary dissociation AC -> A+C, and the ratio of these coupling constants for C and B, respectively.
These numbers are formally necessary to describe all possible forms of interactions between these sites, but I doubt that they can be extracted from sedimentation velocity experiments. In the absence of information to the contrary, at least initially, it is possible to use the parsimonious assumption that the forms of cooperativity are absent, in which case the numeric value of these fields for the ratio of rate constants can be set to zero.

Like in the other models, the values for the parameters that are irrelevant should not be floated. For example, all enthalpy values should not be fitted except when analyzing ITC data (in which case the kinetic rate constant fields become meaningless).
A+B+B+C <--> AB +B+C <--> BAB + C <--> AC + B+B <--> ABC + B <--> BABC
This is a variation on the previous model where A has two binding sites for B.
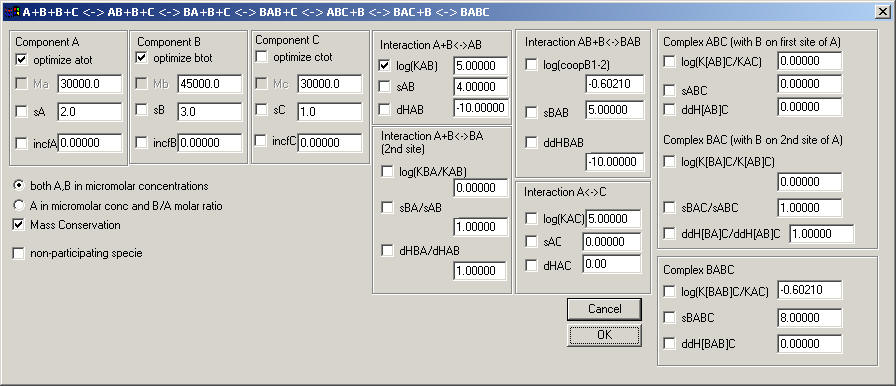
The two binding sites for B on A can have different affinity (expressed through the ratio KBA/KAB, where equal sites would have log(KAB/KBA) = 0), and additionally there may be cooperativity (for macroscopic constants, the statistical factor for non-cooperative binding would be log(coopB1-2) = -0.6 [remember these are base 10 logs, and log10(1/4) = -0.6021]).
Further, there can be cooperativity of the first binding site for B on binding of C, same for the second site for B on binding of C, and finally for double ligand A by B on binding of C.
A+B+B+C+C <--> A + BC + BC <--> AB +B+C+C <--> BAB + C +C <--> BABC +C <--> CBABC
This model is different from the previous in that C is not interacting with A directly, but only with B.

The binding constant of B<-->C can depend on whether B is bound to A or not. This can be different for the first site for B on A and the second site for B on A, as well as when both sites are occupied.
All models provide the possibility of adding an additional species that is unrelated to the reactive species.

This can be used to describe, for example, a contaminant, or IF signals from sedimenting buffer salts. The presence of such components, and their estimated molar mass and s-value may be obtained from c(s) analysis with sedfit. The purpose of the vbar in this section allows this species to be used in a flexible way in density contrast experiments (e.g. to describe the free detergent micelle).